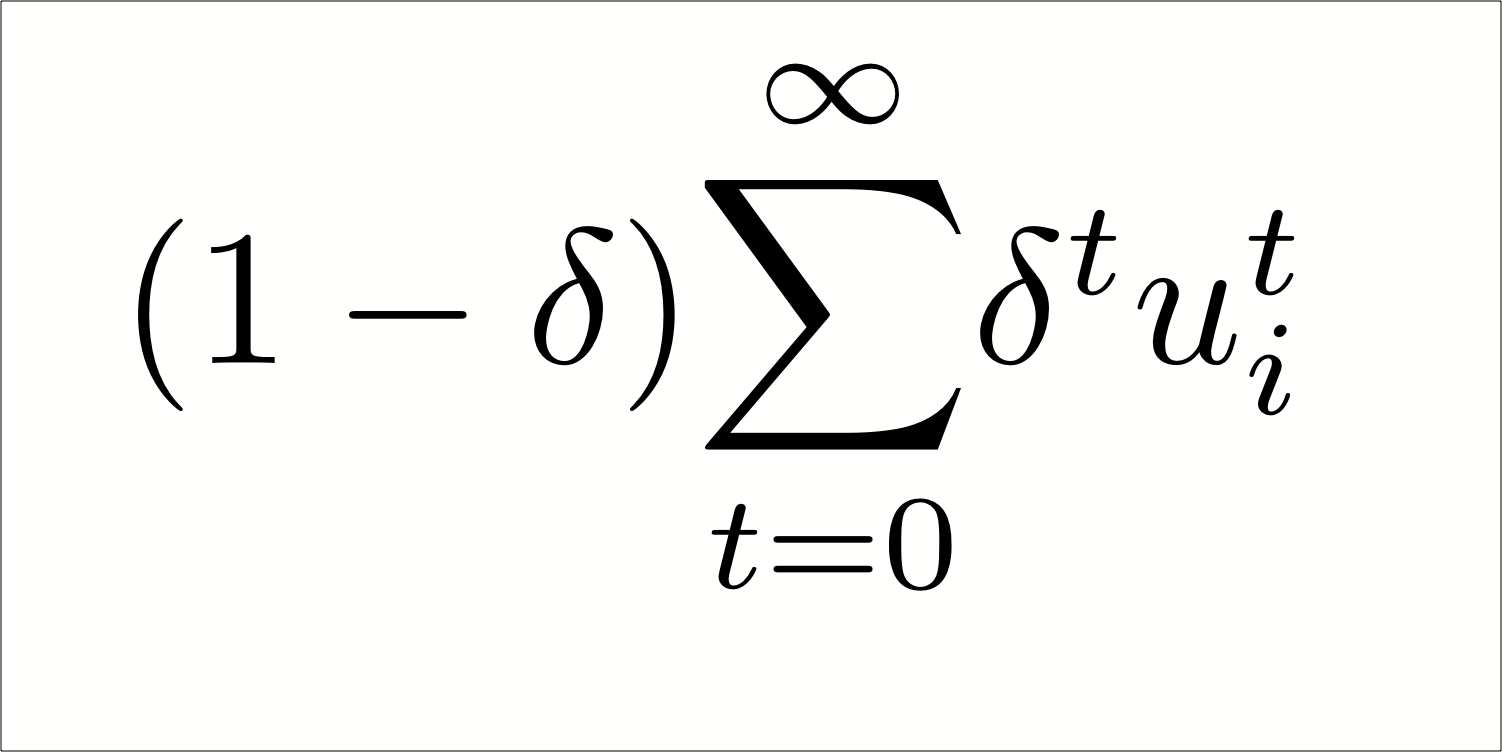Category: Game Theory

Chapter 5.2 of Jim Ratliff’s graduate-level game-theory course. When the stage game is repeated infinitely, we ensure the finiteness of the repeated-game payoffs by introducing discounting of future payoffs relative to earlier payoffs. Such discounting can be an expression of time preference and/or uncertainty about the length of the game. We introduce the average discounted payoff as a convenience which normalizes the repeated-game payoffs to be “on the same scale” as the stage-game payoffs. Infinite repetition can be key to obtaining behavior in the stage games which could not be equilibrium behavior if the game were played once or a known finite number of times. We show that cooperation is a Nash equilibrium of the infinitely repeated prisoners’ dilemma for sufficiently patient players. We show that cooperation in every period by both players is a subgame-perfect equilibrium of the infinitely repeated prisoners’ dilemma for sufficiently patient players.

Chapter 5.3 of Jim Ratliff’s graduate-level game-theory course. A “folk theorem” in repeated-game theory is a characterization of the set of average payoffs in a class of games that are achievable in a given type of equilibrium. The strongest folk theorems are of the following loosely stated form: “Any strictly individually rational and feasible payoff vector of the stage game can be supported as a subgame-perfect equilibrium average payoff of the repeated game.” These statements often come with qualifications such as “for discount factors sufficiently close to 1” or, for finitely repeated games, “if repeated sufficiently many times.” We precisely define the terms feasible and individually rational. We state and prove two folk theorems, one Nash and one perfect, which have the virtue of being relatively easy to prove because their proofs rely only on simple “grim trigger” strategies. Then we will prove a perfect folk theorem stronger than the first two using more complicated strategies.

Chapter 6.1 of Jim Ratliff’s graduate-level game-theory course. A game of incomplete information, or a Bayesian game, is one where at least one player begins the game with private information, which is described by a player’s type. Each player knows her own type with complete certainty and has common-knowledge beliefs about other players’ types. A strategy for a player in the incomplete-information game is a strategy for each of that player’s types in a corresponding strategic-form game. A Bayesian equilibrium of a static game of incomplete information is a strategy profile such that every type of every player is maximizing her expected utility given the type-contingent strategies of her opponents and the probability distribution over types of each player. We consider an example from industrial-organization.

Chapter 6.2 of Jim Ratliff’s graduate-level game-theory course. Sender-receiver games are the simplest dynamic games of incomplete information. There are only two players, Sender and Receiver. Sender chooses a message m from a message space M, which Receiver observes and then responds by choosing an action a from his action space A. The Sender has private information; she can have one of two types. The Receiver has no private information and has common-knowledge prior beliefs about the Sender’s type. We define what a strategy for each player is and what a strategy profile for the game is. We define conditions on a strategy profile in order that it be a perfect Bayesian equilibrium (PBE) of the game. We consider two refinements of PBE: the Test of Dominated Messages and the Intuitive Criterion.

Even subgame perfection permits undesirable equilibria of extensive-form games. Perfect Bayesian equilibrium is a refinement of subgame perfection defined by four Bayes Requirements. These requirements can eliminate bad subgame-perfect equilibria by requiring players to have beliefs, at each information set, about which node of the information set she has reached, conditional on being informed she is in that information set.